5 Indexing and searching

  Locators are pointers into data. They contain two components: a tuple identifier and a leaf identifier. Each tuple in a relation can be located with its tuple identifier. Each leaf within a given tuple is uniquely identified by its leaf identifier.

Qddb associates a list of locators with every key, that is, every searchable value found in the tuples. We call this association the index into a Qddb relation. The index can be accessed in three ways. The most direct way is by hashing the given key to find the associated locator list. Word-range and numeric-range searches are performed by binary search in a sorted key or number file, leading to a contiguous set of entries, each of which points to a locator list in the index. Regular-expression searches use finite-automaton search through the sorted key file, leading to a set of matching entries, each of which points to a locator list in the index.

In all cases, searches yield a list of locators. If only the list of tuples is needed, this list can be pruned by discarding duplicate locators that have the same tuple identifier. If the search is to be constrained to particular attributes, the list of locators is pruned by discarding all locators with irrelevant leaf identifiers.

Complex searches are constructed by applying simple searches and combining the results. We will demonstrate several examples based on this schema tree:

        Name (First Last) Address (Street City)*

A sample complex query might be: Find all tuples with the value ``Joe'' in the Name.First field and ``Harrison'' in the Name.Last field. In other words, we want to find tuples that satisfy the following expression:

        (Name.First = "Joe") and (Name.Last = "Harrison")

This query requires three steps: (1) Search for all tuples with Name.First containing ``Joe'', (2) Search for all tuples with Name.Last containing ``Harrison'', and (3) construct a weak intersection of the matching locators. A weak intersection ignores the leaf identifiers of the locators and uses only the tuple identifiers for comparisons. Only tuples that match both searches remain after the intersection.

Strong operations on locator lists do not ignore the leaf identifiers. Strong operations use both the tuple identifier and the leaf identifier for comparison purposes. Two locators are equivalent if both the tuple identifiers and leaf identifiers are identical. For example, a strong intersection of sets A and B produces all locators that reside in both sets; a weak intersection produces all locators with tuple identifier t if at least one locator with tuple identifier t resides in both A and B. Strong operations generally operate on lists that contain locators associated with a particular attribute.

We can also do binary union and exclusion operations on locator lists. Binary union merges two sets of locators. Binary exclusion of two sets A and B produces all locators that are contained in set A but not in set B. Binary exclusion has both weak and strong forms. Binary union does not have a weak or strong form because no comparisons are used in the operation.

Suppose, for example, we want to find all occurrences of ``Joe'' in the Name.First field where the Name.Last field is not ``Harrison''. In other words, we want

    (Name.First = "Joe") and ((Name.Last = ".*") 
        minus (Name.Last = "Harrison"))

The syntax ``.*'' means ``any value.'' The search first builds the locator lists (A, B, and C) for the three subexpressions from left to right; it then performs a strong exclusion (B-C) and a weak intersection ( ) to produce the result.

5.1 Finding tuples with matching rows

  In our previous example, the attributes of interest were not expandable. Expandable attributes provide an interesting dilemma: how do we know if two matching locators belonging to the same tuple are in the same row? To illustrate this problem, consider the query:

        (Address.Street = "Rainbow") and (Address.City = "Lexington")

A tuple may have the following values for the Address attribute:

Address.Street Address.City

Rainbow Pittsburgh

Nichols Lexington

Such a tuple will be produced by the weak intersection of the two expressions, but is not a proper result, because the two expressions fail to match on the same row.

For two leaves to be in the same row, they must be in the same instance of their deepest common attribute ancestor. In our case, they must be in the same instance of Address. (In the previous cases, they must be in the same instance of Name, but this attribute is not expandable, so all results were in the same row.)

We can determine whether two leaves are in the same row by (1) comparing the leaf identifiers of the two leaves from left to right, and (2) noticing the first position that the attribute numbers (odd positions) or instance numbers (even positions) differ. If the first difference is an attribute number, then the two leaves are in the same row. If the first difference is an instance number, then the two leaves are not in the same row.

Suppose we perform a query Q that returns a set of locators L describing the results of our query. We want to find all rows that match our query Q. The following algorithm accomplishes this task:

1. Let T be the set of all tuple trees in the relation.
2. Let A represent all attributes in the schema tree that were used in our query Q.
3. Partition the set L into a set S of subsets. Each subset contains all locators describing a single tuple ; that is, there is a one-to-one correspondence from each element to an element .
4. For each ,
   1. For each attribute , place all locators describing attribute a (regardless of instance) into a set . A set if and only if there is no locator describing a match on attribute a.
   2. If for any attribute , , then the tuple tree t described by s does not contain a row that satisfies Q. Let S=S-s, then continue with the next .
   3. Otherwise, perform the cartesian product .
   4. For each , check to see if all locators in the components of r are in the same row. If no satisfies this condition, then the tuple tree t described by s does not contain a row matching query Q; let S=S-s and continue with the next . Otherwise, do not modify S and continue with the next .

At the completion of this algorithm, each remaining describes all rows in a single tuple that satisfy Q. For each , we can find the all tuples that satisfy Q by the tuple identifier contained in any locator . We now have a set of tuple identifiers completely describing the locations of the tuple trees satisfying query Q.

This algorithm finds all tuples with at least one matching partial row (partial in that it considers only the attributes in the query) without reading the actual tuple tree data. Each matching row may represent several complete rows; this expansion can be determined only by reading the data. For most purposes, this is a very efficient mechanism for determining which tuples match a particular query; we only need to read the tuples that contain at least one matching row.

5.2 Generating matching rows

  After applying the algorithm presented in Section 5.1, we have a set S that contains a subset of locators for each tuple satisfying our query Q. Each subset s describes all the locators for each attribute in a particular tuple matching our query. We know each tuple is guaranteed to contain at least one row satisfying our query. We must now read the tuple's leaves from the disk to build the tuple tree and produce all matching rows. Once we have the tuple in the form of a tuple tree, we mark all leaves matching our query as good. We mark bad all leaves of searched attributes that are not marked good, because we know that these leaves did not match our query. A traversal of the tuple tree will produce all rows matching the query if we exclude any row containing a leaf that is marked bad.

  
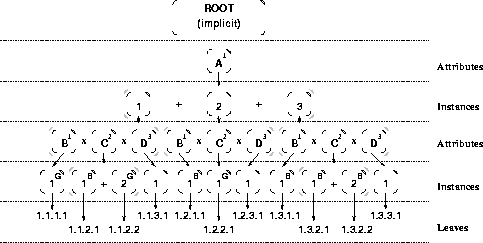
Figure 4: Generating rows in a tuple tree matching a query.

For example, suppose we have the tuple tree shown in Figure 4 and we search on the attributes A.B and A.C. Suppose we know this tuple matches because the algorithm presented in Section 5.1 produces a subset corresponding to this tuple. Suppose our set s describes the leaves ( ), so we mark those leaves as good. (Figure 4 shows them with a superscript `G'.) The searched attributes are A.B and A.C, so we mark all instances of A.B and A.C that are not marked good as bad (shown with a superscript `B'.)

To produce all rows matching the query for this tuple, we use the following modification of the algorithm presented in Section 4.3:

    procedure ProduceAttributes (AttributeNode) : set of rows
        answer := NULL
        for each Inst := instance of AttributeNode do
            answer := union(answer, ProduceInstances(Inst))
        return answer

    procedure ProduceInstances (InstanceNode) : set of rows
        if leaf(InstanceNode) then
            if bad(InstanceNode) then
                return NULL
            else
                return InstanceNode.Value
        else
            answer := NULL
            for each Attr := attribute of InstanceNode do
                answer := cartesian product(answer, 
                    ProduceAttributes(Attr))
            return answer

Using the above algorithm on the tuple shown in Figure 4, we get the following single row:

1.1.1.1 1.1.2.2 1.1.3.1

The other rows were eliminated because one or more of their leaves were marked bad. This algorithm will not generate false matches because each leaf that represents a searched attribute is marked bad unless a locator is found for that particular leaf.

5.3 Efficiency

Tuple trees are generally stored contiguously. Each tuple tree contains all the relational rows logically related to that tuple, so the following tasks are greatly simplified:

1. Reading - tuple trees can be read in a single file system read operation, so all rows related to that tuple are available for processing.
2. Locking - tuple trees can be locked by a single file system lock operation.
3. Writing - tuple trees can be written with a single file system write operation.
4. Addition - tuple trees (or any sub-tree) can be added with a single operation on an in-memory tuple tree.
5. Deletion - tuple trees (or any sub-tree) can be deleted with a single operation on an in-memory tuple tree.

Tuple trees need not store empty attributes, either in memory or in a file, so sparse tables may be represented in a very compressed form. The main disadvantage of the tuple tree is that leaf identifiers must also be stored with each attribute value in the tuple. To eliminate much of this overhead, we can enumerate all possible leaf identifiers with base-36 indices (

) and store the index instead of the full leaf identifier. For example, (1,679,616) unique leaf identifiers can be represented by 4 digits (a 4-byte overhead per attribute). In practice, tuple trees tend to have a high level of leaf identifier replication between different tuple trees, so the number of unique leaf identifiers is typically quite small.